Tag: strength

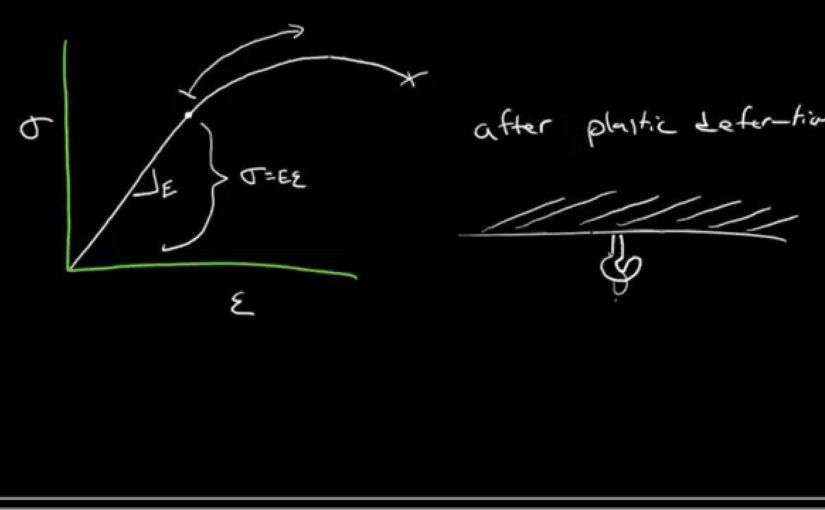
 So we’ve sketched stress-strain. A curve like this for typical metal. And we know an equation within the linear elastic region. That’s before the proportional limit. And that’s, of course, Hooke’s Law– sigma equals E times epsilon. But what do we have after plastic deformation? How can we perform calculations after plastic deformation? If, for example, we had something that– a bolt in the ceiling– oh, that’s a horrendous drawing. Let’s fix that. Let’s fix that before I lose my job. So here’s– that’s even worse. Oh, my goodness. OK. This is good. No, that’s still awful. But there’s a hook and, I don’t know, something is hanging from it. I was going to draw a force so I don’t have to draw something else. There’s a hook hanging from the ceiling and you apply a force to it and you want to know, well, how much does that tie– that’s what that is– it’s called intention– that tensile tie– elongate? What’s its distance? What’s its length? And, well, you can only, at this point, do calculations if the force results in a stress that’s less than the yield strength. If it’s more than that, while it’s classically deformed, we couldn’t deal with it unless we had some kind of way of describing the shape of the curve after it leaves the linear elastic region. And it’s nice. We do have an equation that fits the curve. But it’s going– we can’t use engineering stress. We have to use what’s called true stress. So that’s what I’d like to introduce to you right now. So again, we’re going to take a look at a generalized sample here. And the idea– the goal– is of course that we’re going to go to be able to this– calculate and understand plastic deformation. So here’s our sample with its initial cross-sectional area as we’ve discussed before. And we said, well, when you load it, it gets longer and gets narrower. And it’s that reduction in the cross-sectional area that we’re interested in. This area here now, we could call it an instantaneous area. Whereas this area, the white one, was the initial area. The initial area was what we started with. But then while the load is applied– sorry, let me draw the force in. While the load is applied, the cross-sectional area has decreased. So the first thing you could do is we could say, all right, well, that means that this material itself is experiencing a force over a smaller area. So we could define the true stress as the force over that actual cross-sectional area. This is the true stress. This is the stress that the material itself is feeling. OK? And that subscript I am telling us this is the instantaneous cross-sectional area. Instantaneous. I can’t do more than one thing at the same time. Instantaneous– I missed a U– cross-sectional area. Instantaneous cross-sectional area. And I’ll show you what the plot would look like in just a moment. We could also do the same thing for the strain, although that’s going to be just a little bit– require a little bit more thinking. The true strain has to account for the fact that what we’re doing is we’re applying a change in length. Right? We’re elongating it over a certain length. The very first little bit of elongation is elongation over l0. But then, after that, the elongation is elongated over the previous length which was l0 plus that little delta l.  And so if you do that for infinitely small– infinitesimally small changes in length, the way we would write that is we’d have to say, the true strain, what we’re doing is we’re integrating. We’re integrating those infinitesimally small changes in length– that’s dl– by l from l0– the initial length– to the instantaneous length. And so if we do that, you find that you have ln of l instantaneous minus length 0, which is ln of l instantaneous over l0. So we have another equation there. I’ll put a box around that. So this is the true strain. True strain. And if we take that true stress and we plot it against the true strain, I’ll show you what we get. Let me just plot stress and strain and I’ll show you what we’ve already seen. That’s the engineering stress-strain curve. And then what I’ll do is I’ll plot for you– after it starts to plastically deform the– ran out of space there– the true stress– so this one here– continues to increase. It doesn’t have that decrease at the UTS. That’s the true stress true strain curve. And this one is, of course, engineering. The nice thing about this plot is once you’ve got true stress and true strain, we can fit that data quite nicely for most metals with a simple equation. And that is true stress is equal to this coefficient times the true strain raised to the power n. So that’s an equation that fits that true stress true strain data quite nicely. And what’s useful about this is these are constants. That’s the constant n– I’ll define it for you in a moment– and this K is also a constant. Those are material properties. We can look those up in an engineering handbook. So n is called the– well, this equation is called the strain-hardening equation. Strain hardening equation. And strain hardening– hardening correlates to– hardness correlates to strength. So really this is the equation that’s telling us that we’re strengthening the material and we’ve got the strain hardening exponent and the strain hardening coefficient K.As found on YouTubeExplaindio Agency Edition FREE Training How to Create Explainer Videos & SELL or RENT them! Join this FREE webinar | Work Less & Earn More With Explaindio AGENCY EDITION