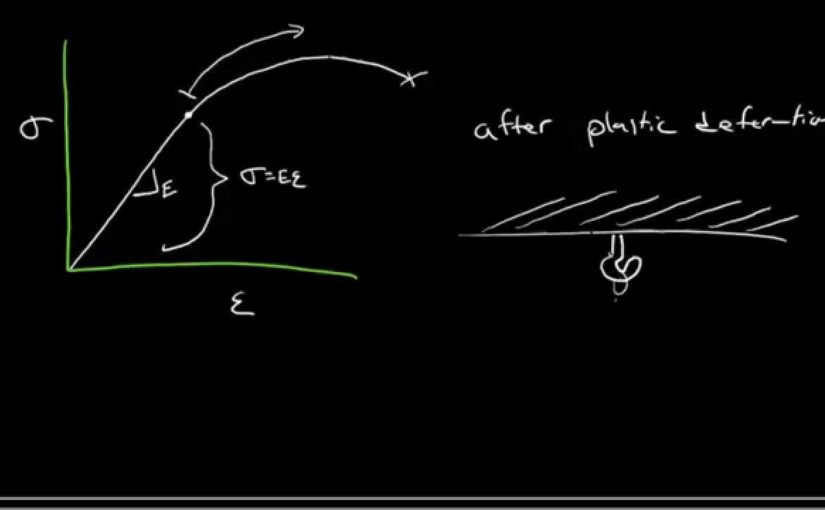
So we’ve sketched stress-strain. A curve like this
for typical metal. And we know an equation within
the linear elastic region. That’s before the
proportional limit. And that’s, of course,
Hooke’s Law– sigma equals E times epsilon. But what do we have after
plastic deformation? How can we perform calculations
after plastic deformation? If, for example,
we had something that– a bolt in
the ceiling– oh, that’s a horrendous drawing. Let’s fix that. Let’s fix that
before I lose my job. So here’s– that’s even worse. Oh, my goodness. OK. This is good. No, that’s still awful. But there’s a hook
and, I don’t know, something is hanging from it. I was going to draw
a force so I don’t have to draw something else. There’s a hook hanging
from the ceiling and you apply a
force to it and you want to know,
well, how much does that tie– that’s
what that is– it’s called intention– that
tensile tie– elongate? What’s its distance? What’s its length? And, well, you can only, at this point, do calculations
if the force results in a stress that’s
less than the yield strength. If it’s more than that, while
it’s classically deformed, we couldn’t deal
with it unless we had some kind of
way of describing the shape of the
curve after it leaves the linear elastic region. And it’s nice. We do have an
equation that fits the curve. But it’s going– we can’t
use engineering stress. We have to use what’s
called true stress. So that’s what I’d like to
introduce to you right now. So again, we’re going to take
a look at a generalized sample here. And the idea– the
goal– is of course that we’re going to go to
be able to this– calculate and understand
plastic deformation. So here’s our sample with its
initial cross-sectional area as we’ve discussed before. And we said, well,
when you load it, it gets longer
and gets narrower. And it’s that reduction in
the cross-sectional area that we’re interested in. This area here now, we could
call it an instantaneous area. Whereas this area, the white
one, was the initial area. The initial area was
what we started with. But then while the load
is applied– sorry, let me draw the force in. While the load is applied,
the cross-sectional area has decreased. So the first thing
you could do is we could say, all right, well, that
means that this material itself is experiencing a
force over a smaller area. So we could define
the true stress as the force over that
actual cross-sectional area. This is the true stress. This is the stress that
the material itself is feeling. OK? And that subscript
I am telling us this is the instantaneous
cross-sectional area. Instantaneous. I can’t do more than one thing
at the same time. Instantaneous– I missed a
U– cross-sectional area. Instantaneous cross-sectional area. And I’ll show you
what the plot would look like in just a moment. We could also do the same
thing for the strain, although that’s going to be
just a little bit– require a little bit more thinking. The true strain has to
account for the fact that what we’re doing is we’re
applying a change in length. Right? We’re elongating it
over a certain length. The very first little
bit of elongation is elongation over l0. But then, after
that, the elongation is elongated over the
previous length which was l0 plus that little delta l.

And so if you do that
for infinitely small– infinitesimally small
changes in length, the way we would write that
is we’d have to say, the true strain, what we’re
doing is we’re integrating. We’re integrating those
infinitesimally small changes in length– that’s dl– by l
from l0– the initial length– to the instantaneous length. And so if we do that,
you find that you have ln of l instantaneous
minus length 0, which is ln of l instantaneous over l0. So we have another
equation there. I’ll put a box around that. So this is the true strain. True strain. And if we take that true
stress and we plot it against the true strain,
I’ll show you what we get. Let me just
plot stress and strain and I’ll show you what
we’ve already seen. That’s the engineering
stress-strain curve. And then what I’ll do is I’ll
plot for you– after it starts to plastically deform the–
ran out of space there– the true stress– so this one
here– continues to increase. It doesn’t have that
decrease at the UTS. That’s the true stress
true strain curve. And this one is, of
course, engineering. The nice thing
about this plot is once you’ve got true
stress and true strain, we can fit that data
quite nicely for most metals with a simple equation. And that is true stress
is equal to this coefficient times the true strain
raised to the power n. So that’s an equation that fits
that true stress true strain data quite nicely. And what’s useful about
this is these are constants. That’s the constant n– I’ll
define it for you in a moment– and this K is also a constant. Those are material properties. We can look those up in
an engineering handbook. So n is called the–
well, this equation is called the
strain-hardening equation. Strain hardening equation. And strain hardening– hardening
correlates to– hardness correlates to strength. So really this is
the equation that’s telling us that we’re
strengthening the material and we’ve got the
strain hardening exponent and the strain
hardening coefficient K.
As found on YouTubeExplaindio Agency Edition FREE Training How to Create Explainer Videos & SELL or RENT them! Join this FREE webinar | Work Less & Earn More With
Explaindio AGENCY EDITION
 And so if you do that
for infinitely small– infinitesimally small
changes in length, the way we would write that
is we’d have to say, the true strain, what we’re
doing is we’re integrating. We’re integrating those
infinitesimally small changes in length– that’s dl– by l
from l0– the initial length– to the instantaneous length. And so if we do that,
you find that you have ln of l instantaneous
minus length 0, which is ln of l instantaneous over l0. So we have another
equation there. I’ll put a box around that. So this is the true strain. True strain. And if we take that true
stress and we plot it against the true strain,
I’ll show you what we get. Let me just
plot stress and strain and I’ll show you what
we’ve already seen. That’s the engineering
stress-strain curve. And then what I’ll do is I’ll
plot for you– after it starts to plastically deform the–
ran out of space there– the true stress– so this one
here– continues to increase. It doesn’t have that
decrease at the UTS. That’s the true stress
true strain curve. And this one is, of
course, engineering. The nice thing
about this plot is once you’ve got true
stress and true strain, we can fit that data
quite nicely for most metals with a simple equation. And that is true stress
is equal to this coefficient times the true strain
raised to the power n. So that’s an equation that fits
that true stress true strain data quite nicely. And what’s useful about
this is these are constants. That’s the constant n– I’ll
define it for you in a moment– and this K is also a constant. Those are material properties. We can look those up in
an engineering handbook. So n is called the–
well, this equation is called the
strain-hardening equation. Strain hardening equation. And strain hardening– hardening
correlates to– hardness correlates to strength. So really this is
the equation that’s telling us that we’re
strengthening the material and we’ve got the
strain hardening exponent and the strain
hardening coefficient K.As found on YouTubeExplaindio Agency Edition FREE Training How to Create Explainer Videos & SELL or RENT them! Join this FREE webinar | Work Less & Earn More With Explaindio AGENCY EDITION
And so if you do that
for infinitely small– infinitesimally small
changes in length, the way we would write that
is we’d have to say, the true strain, what we’re
doing is we’re integrating. We’re integrating those
infinitesimally small changes in length– that’s dl– by l
from l0– the initial length– to the instantaneous length. And so if we do that,
you find that you have ln of l instantaneous
minus length 0, which is ln of l instantaneous over l0. So we have another
equation there. I’ll put a box around that. So this is the true strain. True strain. And if we take that true
stress and we plot it against the true strain,
I’ll show you what we get. Let me just
plot stress and strain and I’ll show you what
we’ve already seen. That’s the engineering
stress-strain curve. And then what I’ll do is I’ll
plot for you– after it starts to plastically deform the–
ran out of space there– the true stress– so this one
here– continues to increase. It doesn’t have that
decrease at the UTS. That’s the true stress
true strain curve. And this one is, of
course, engineering. The nice thing
about this plot is once you’ve got true
stress and true strain, we can fit that data
quite nicely for most metals with a simple equation. And that is true stress
is equal to this coefficient times the true strain
raised to the power n. So that’s an equation that fits
that true stress true strain data quite nicely. And what’s useful about
this is these are constants. That’s the constant n– I’ll
define it for you in a moment– and this K is also a constant. Those are material properties. We can look those up in
an engineering handbook. So n is called the–
well, this equation is called the
strain-hardening equation. Strain hardening equation. And strain hardening– hardening
correlates to– hardness correlates to strength. So really this is
the equation that’s telling us that we’re
strengthening the material and we’ve got the
strain hardening exponent and the strain
hardening coefficient K.As found on YouTubeExplaindio Agency Edition FREE Training How to Create Explainer Videos & SELL or RENT them! Join this FREE webinar | Work Less & Earn More With Explaindio AGENCY EDITION