There are
a few other things that we can determine
from the stress-strain curve of metal that
is quite interesting. And I’d like to just spend
a moment looking at that. So again, we’ve got
the stress here, on the vertical axis,
strain– typical metal. We have a curve that
looks something like this. It comes up looking linear
elastic, plastic, ultimate tensile strength,
and then fracture. And so we’ve determined
all of the strengths. We have the yield strength,
the ultimate tensile strength, and the fracture strength. But what other properties
can we determine? Well, first of all, one of them
that you may have heard about is the ductility. So ductility has a usage
in common language. You might say, well,
what’s ductility all about? If something’s very ductile,
you might say, well, it describes how much you
can stretch something. But of course, we
know that that’s not accurate enough. Stretch, is that referring
to elastic or plastic? So we’ve got to be
better than that. And in fact, I’ll
tell you ductility is a measure of a plastic strain. So we know
it’s a strain quantity, and it refers to plastic
deformation, only plastic strain to fracture. Now we’ve got something we
can work with– plastic strain to fracture. So let’s see well, this
is the point of fracture. That’s a fracture. So that fracture,
if we unload we’d have a value here
for total strain. Let me write that in there
for you, total strain. If we unloaded– if we
took the total strain there at fracture, just a moment
before it fractured, that would be our total strain. But what if we unloaded it? Somehow you knew just
infinitesimally before it was going to fracture– well,
we know that Young’s modulus is structure-independent. So it won’t change. So we would have unloaded
that same modulus. This means we come back down
here to a value on the strain axis, a finite value
corresponding to zero stress. It’s unloaded, there’s
no stress on it, but there’s still some
persistent strain. That strain has to be plastic. That’s a plastic strain, which
means that this strain here is elastic. That’s elastic, and that makes
sense because what is that? That’s the strain underneath
this linear unloading portion. And the unloading
portion, if it’s linear, is governed by Hooke’s law. And we know that’s elastic
because Hooke’s law refers to elastic behavior. So if we unload down and
we get plastic strain, that plastic strain has
got to be the ductility. So ductility, you
unload at fracture. And the remaining
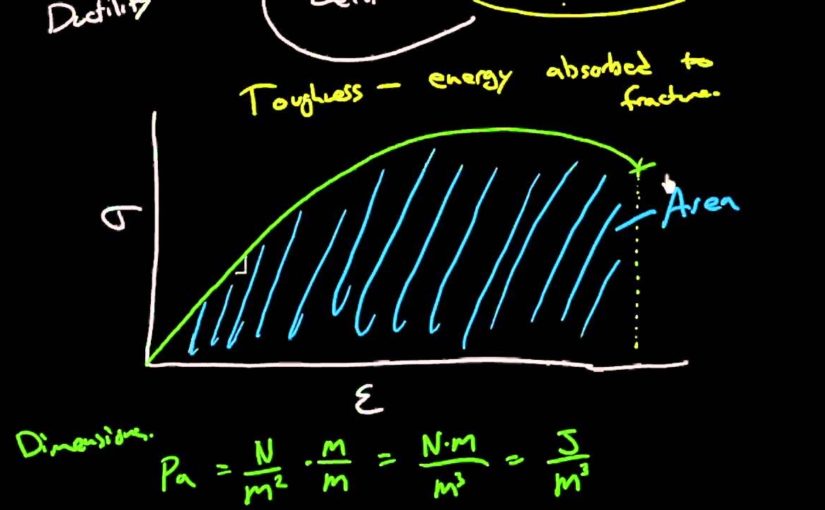
strain is the ductility. Another interesting property
that we can determine from this stress-strain
behavior for a metal, for other material classes as
well, is called toughness. And the toughness is sometimes
not such an intuitive quantity. You can understand strength,
it’s force over area. You got a sense for that. It’s pressure, if you will. Even modulus you can kind
of get a bit of an intuitive sense for it because
it’s how hard is it to bend
something elastically. It’s a little harder, but
the toughness is– toughness, I’ll tell you what the tough is. Toughness is the energy–
it’s an energy term. And it’s energy
absorbed to fracture. What we can do
is integrate. And that is to take the
area under the curve. So if we take the area
under this curve here, it would be this area here, all
this area here under the curve is the toughness.

And how do we know that? We could look at
it dimensionally. If we’re taking a product
of stress and strain and looking at the dimensions,
stress has units of Pascals. And what’s a Pascal? A Pascal is a Newton
per square meter. Well, I can go on living
my life multiplying whatever I want by 1 and just
multiply this screen by 1. You didn’t even notice. So here we go, where I multiply
Newton per square meter by 1, meter over meter, and I
end up with a familiar term in the numerator– Newton meter. And of course in the denominator
I’ve got volume units. But what’s the Newton meter? A Newton meter is
nothing more than a joule. So we’ve now got
joules per volume as units when we
integrate under this. And that’s great because
we want an energy unit. So if we integrate under the
entire curve up to fracture, it tells us how much energy
went into fracturing that. And that includes elastic
and plastic deformation. The final thing that we
can obtain from the stress curve, is
another energy unit and it’s quite useful– it’s
a stored energy unit this time. We’ve got stress and strain. We’ve got our linear elastic
region, plastic deformation, and fracture– is
the resilience. Thus resilience
is a measure of the stored elastic strain
energy at the yield strength. So again, we know if it’s going
to be an energy term, energy per volume for a given
volume of material, we’re going to have to
integrate under the curve. And where are we
going to do it from? Well, we’ll go to
the yield strength. And we go down from there. And if we unloaded at
the yield strength– I’m going to be a little
careful about something– if we unloaded at the
yield strength, you’d find that you have
a little sliver of permanent or plastic strain. Maybe it’s close to
the 0.2% offset strain. You’d probably have some plastic
strain accumulated when we had yield. For practical purposes, we say
it’s elastic before yielding and it’s plastic after. You might have a sliver. So we’re not going to
include that if we’re going to be strict with
our definition here. And so that area there
is the resilience. And that area is
just an area of a triangle. And we know that the
area of a triangle is 1/2 base times
height, which in our case is 1/2 of– well,
what’s the base? The base is the elastic strain. And that’s good because we’re
after the stored elastic strain energy. So we’ve got strain elastic. And what’s the height? Well, the height is
the yield strength. But we can, again,
do better than this. Because if it’s elastic,
it’s the area under this– or it’s the strain underneath
this linear unloading portion. And the linear
unloading portion, we have a mathematical
equation for. We have stress equals
E times strain. It’s a straight line. So that means that
the strain is going to be equal to sigma over
E. And we fire that in here, and we find that
the resilience is– I should erase that–
the resilience is going to be 1/2 of sigma,
and this is the sigma yield. That’s what we’re using here. So that’s sigma yield
over E times sigma yield. So at the end of the day, the
resilience, which we often use this– I’ll introduce
this symbol here. The full name for this
is the modulus of resilience. And modulus is just a fancy
word for a special number. So our special number here
is the modulus of resilience. And we use the
uppercase letter U. Is 1/2 sigma yield
squared upon E– and that’s an interesting
little equation. It tells you the stored
strain energy for a material. So if you’re going to make
a material for a spring, you’d look for something with
a high modulus of resilience. And again, the units
here, the dimensions here of modulus of
resilience are going to be joules per cubic meter.
As found on YouTubeExplaindio Agency Edition FREE Training How to Create Explainer Videos & SELL or RENT them! Join this FREE webinar | Work Less & Earn More With
Explaindio AGENCY EDITION
 And how do we know that? We could look at
it dimensionally. If we’re taking a product
of stress and strain and looking at the dimensions,
stress has units of Pascals. And what’s a Pascal? A Pascal is a Newton
per square meter. Well, I can go on living
my life multiplying whatever I want by 1 and just
multiply this screen by 1. You didn’t even notice. So here we go, where I multiply
Newton per square meter by 1, meter over meter, and I
end up with a familiar term in the numerator– Newton meter. And of course in the denominator
I’ve got volume units. But what’s the Newton meter? A Newton meter is
nothing more than a joule. So we’ve now got
joules per volume as units when we
integrate under this. And that’s great because
we want an energy unit. So if we integrate under the
entire curve up to fracture, it tells us how much energy
went into fracturing that. And that includes elastic
and plastic deformation. The final thing that we
can obtain from the stress curve, is
another energy unit and it’s quite useful– it’s
a stored energy unit this time. We’ve got stress and strain. We’ve got our linear elastic
region, plastic deformation, and fracture– is
the resilience. Thus resilience
is a measure of the stored elastic strain
energy at the yield strength. So again, we know if it’s going
to be an energy term, energy per volume for a given
volume of material, we’re going to have to
integrate under the curve. And where are we
going to do it from? Well, we’ll go to
the yield strength. And we go down from there. And if we unloaded at
the yield strength– I’m going to be a little
careful about something– if we unloaded at the
yield strength, you’d find that you have
a little sliver of permanent or plastic strain. Maybe it’s close to
the 0.2% offset strain. You’d probably have some plastic
strain accumulated when we had yield. For practical purposes, we say
it’s elastic before yielding and it’s plastic after. You might have a sliver. So we’re not going to
include that if we’re going to be strict with
our definition here. And so that area there
is the resilience. And that area is
just an area of a triangle. And we know that the
area of a triangle is 1/2 base times
height, which in our case is 1/2 of– well,
what’s the base? The base is the elastic strain. And that’s good because we’re
after the stored elastic strain energy. So we’ve got strain elastic. And what’s the height? Well, the height is
the yield strength. But we can, again,
do better than this. Because if it’s elastic,
it’s the area under this– or it’s the strain underneath
this linear unloading portion. And the linear
unloading portion, we have a mathematical
equation for. We have stress equals
E times strain. It’s a straight line. So that means that
the strain is going to be equal to sigma over
E. And we fire that in here, and we find that
the resilience is– I should erase that–
the resilience is going to be 1/2 of sigma,
and this is the sigma yield. That’s what we’re using here. So that’s sigma yield
over E times sigma yield. So at the end of the day, the
resilience, which we often use this– I’ll introduce
this symbol here. The full name for this
is the modulus of resilience. And modulus is just a fancy
word for a special number. So our special number here
is the modulus of resilience. And we use the
uppercase letter U. Is 1/2 sigma yield
squared upon E– and that’s an interesting
little equation. It tells you the stored
strain energy for a material. So if you’re going to make
a material for a spring, you’d look for something with
a high modulus of resilience. And again, the units
here, the dimensions here of modulus of
resilience are going to be joules per cubic meter.As found on YouTubeExplaindio Agency Edition FREE Training How to Create Explainer Videos & SELL or RENT them! Join this FREE webinar | Work Less & Earn More With Explaindio AGENCY EDITION
And how do we know that? We could look at
it dimensionally. If we’re taking a product
of stress and strain and looking at the dimensions,
stress has units of Pascals. And what’s a Pascal? A Pascal is a Newton
per square meter. Well, I can go on living
my life multiplying whatever I want by 1 and just
multiply this screen by 1. You didn’t even notice. So here we go, where I multiply
Newton per square meter by 1, meter over meter, and I
end up with a familiar term in the numerator– Newton meter. And of course in the denominator
I’ve got volume units. But what’s the Newton meter? A Newton meter is
nothing more than a joule. So we’ve now got
joules per volume as units when we
integrate under this. And that’s great because
we want an energy unit. So if we integrate under the
entire curve up to fracture, it tells us how much energy
went into fracturing that. And that includes elastic
and plastic deformation. The final thing that we
can obtain from the stress curve, is
another energy unit and it’s quite useful– it’s
a stored energy unit this time. We’ve got stress and strain. We’ve got our linear elastic
region, plastic deformation, and fracture– is
the resilience. Thus resilience
is a measure of the stored elastic strain
energy at the yield strength. So again, we know if it’s going
to be an energy term, energy per volume for a given
volume of material, we’re going to have to
integrate under the curve. And where are we
going to do it from? Well, we’ll go to
the yield strength. And we go down from there. And if we unloaded at
the yield strength– I’m going to be a little
careful about something– if we unloaded at the
yield strength, you’d find that you have
a little sliver of permanent or plastic strain. Maybe it’s close to
the 0.2% offset strain. You’d probably have some plastic
strain accumulated when we had yield. For practical purposes, we say
it’s elastic before yielding and it’s plastic after. You might have a sliver. So we’re not going to
include that if we’re going to be strict with
our definition here. And so that area there
is the resilience. And that area is
just an area of a triangle. And we know that the
area of a triangle is 1/2 base times
height, which in our case is 1/2 of– well,
what’s the base? The base is the elastic strain. And that’s good because we’re
after the stored elastic strain energy. So we’ve got strain elastic. And what’s the height? Well, the height is
the yield strength. But we can, again,
do better than this. Because if it’s elastic,
it’s the area under this– or it’s the strain underneath
this linear unloading portion. And the linear
unloading portion, we have a mathematical
equation for. We have stress equals
E times strain. It’s a straight line. So that means that
the strain is going to be equal to sigma over
E. And we fire that in here, and we find that
the resilience is– I should erase that–
the resilience is going to be 1/2 of sigma,
and this is the sigma yield. That’s what we’re using here. So that’s sigma yield
over E times sigma yield. So at the end of the day, the
resilience, which we often use this– I’ll introduce
this symbol here. The full name for this
is the modulus of resilience. And modulus is just a fancy
word for a special number. So our special number here
is the modulus of resilience. And we use the
uppercase letter U. Is 1/2 sigma yield
squared upon E– and that’s an interesting
little equation. It tells you the stored
strain energy for a material. So if you’re going to make
a material for a spring, you’d look for something with
a high modulus of resilience. And again, the units
here, the dimensions here of modulus of
resilience are going to be joules per cubic meter.As found on YouTubeExplaindio Agency Edition FREE Training How to Create Explainer Videos & SELL or RENT them! Join this FREE webinar | Work Less & Earn More With Explaindio AGENCY EDITION